最近拜读算法精品书籍《算法导论》（第三版），在书的第二章使用了一个陌生的符号：θ(g (n))

起初，我认为可能是书籍的印刷错误，或者就是自己知识太狭隘，于是继续读了下去。在书的第三章，详细介绍了各种渐进符号来描述算法的运行时间。主要有五种符号：θ(g (n)) O (g (n)) o (g (n)) Ω(g (n)) ω(g (n))

题述中的 O (g (n)) 就是第二种符号。首先，这五种符号的区别在于各自描述的范围不一样，但它们本质都是一样的。我们将从常见的 O (g (n)) 出发来一一介绍这些符号

# O(g(n))

首先，O (g (n)) 是什么呢？其实它表示了一个函数集合。在《算法导论》中给出了详细的定义：

O(g(n))={f(n)∣存在正常量c和n′,使得对所有n⩾n′,有0⩽f(n)⩽cg(n)}O(g(n))=\{f(n)|存在正常量c和n',使得对所有n\geqslant n',有0\leqslant f(n) \leqslant cg(n)\}

它给出了算法运行时间的一个渐近上界（小于等于）。下图展示了 O 记号背后的直觉知识。（图示来源于《算法导论》）

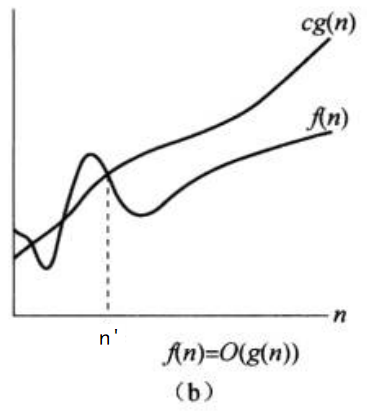
然而，问题又出现了，对于 T (n)=O (g (n))，T (n) 作为一个描述算法运行时间的函数，为什么会和一个集合画上等号呢？书中谈到：“因为 O (g (n)) 是一个集合，所以可以记 f (n)∈O (g (n))，以指出 f (n) 是 O (g (n)) 的成员，作为替代，我们通常记 f (n)=O (g (n)) 来表示相同的概念。因为我们按这种方式活用了等式，所以你可能感到困惑，但在本节的后面我们将看到这样做有其好处。”（来自书中原话，稍作修改）由此看来，T (n)=O (g (n)) 是一种约定俗称，等价于 T (n)∈O (g (n))。

既然 O 记号描述上界，当我们说某某算法运行时间为 O (n^2) 时，意指存在一个属于 O (n^2) 的函数 f (n)，使得对任意的 n，不管选择什么特定的规模为 n 的输入，其运行时间的上界都是 f (n)。这也就是说最坏情况运行时间为 O (n^2)​。

# 其他

到此为止我们知道了 O 表示算法时间复杂度的渐近上界，类似的：

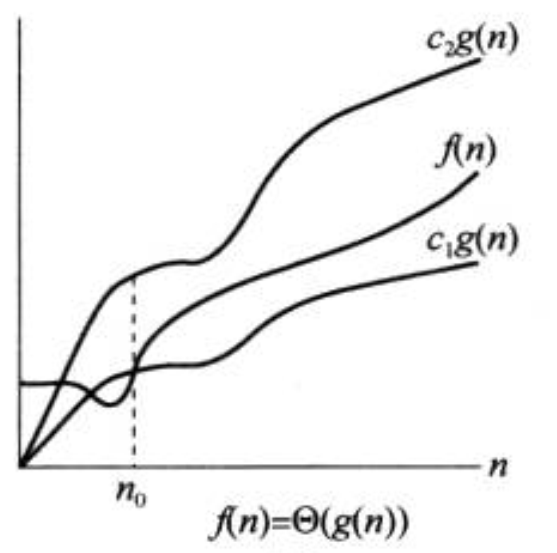
θ 给出了算法运行时间的一个渐近确界，可以理解为夹紧（有夹逼原理的味道）。下图给出了 f (n) 和 g (n) 的直观画面，其中 f (n)=θ(g (n))

4

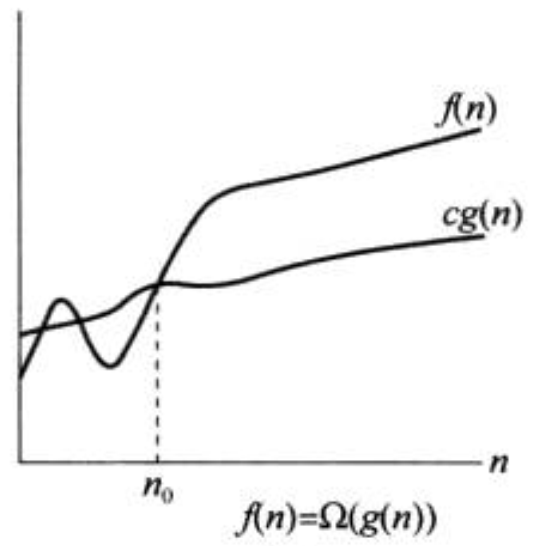
Ω 记号提供了渐近下界，对于给定函数 g (n)，用 Ω(g (n)) 来表示一下函数集合：

Ω(g(n))={f(n)∣存在正常量c和n0,使得对所有n⩾n0,有0⩽cg(n)⩽f(n)}\Omega(g(n))=\{f(n)|存在正常量c和n_{0},使得对所有n\geqslant n_{0},有0\leqslant cg(n) \leqslant f(n)\}

下图给出了直观解释：

5

o 记号表示一个非渐近紧确的上界。可以理解为小于的意思。定义如下

o(g(n))={f(n)∣对任意正常量c,存在正常量n0,使得对所有n⩾n0,有0⩽f(n)<cg(n)}o(g(n))=\{f(n)|对{\color{red}任意}正常量c,存在正常量n_{0},使得对所有n\geqslant n_{0},有0\leqslant f(n) < cg(n)\}

ω\omega 记号与 Ω 记号的关系类似于 o 记号和 O 记号的关系。我们使用ω\omega 记号来表示一个非渐近紧确的下界。定义如下：

ω(g(n))={f(n)∣对任意正常量c,存在正常量n0,使得对所有n⩾n0,有0⩽cg(n)<f(n)}\omega (g(n))=\{f(n)|对{\color{red}任意}正常量c,存在正常量n_{0},使得对所有n\geqslant n_{0},有0\leqslant cg(n) < f(n)\}