# 1. 算法简述

kruskal 是基于贪心思想被设计出来的。此算法得目的是从给定的无向图中获得一棵生成树，并且此生成树得权值之和最小。举个现实中的例子，图的每个顶点都是一个城市，每条边的权值表示两个城市之间的距离，那么现在要铺设铁路，使得每个没做城市都可以互相到达，并且花费的铁轨最少，这个问题就可以用 kruskal 算法求解。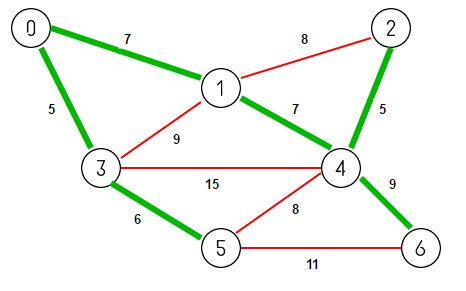
1
常见的最小生成树的算法有 kruskal 和 prim，此文章只叙述前者。

# 2. 算法描述

初始时，我们的最小生成树为空，对于图 G，我们从中找出权值最小的边，有了这条边后，如果把这条边和我们的最小生成树构成回路，那么不能把这条边放入最小生成树中，如果不会构成回路，那么就可以更新我们的最小生成树（把这条边和对应的一对顶点放进去）。重复以上操作，直到遍历完所有的边。

# 3. 代码

在上面的算法描述中，我们需要判断当前的边是否会跟生成树构成回路，对于这个条件判断在使用代码实现时，我们这样转换：
如果这条边的两个顶点都在最小生成树中出现了，那么这条边一定会跟最小生成树构成回路，不能添加到最小生成树中。
所以我们使用数据结构 Edge 来记录每条边的起点，终点和权重，使用 added 数组来表示顶点是否被添加到最小生成树中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
#pragma once
#include <iostream>
#include <string>
#include <algorithm>
#include <vector>

using namespace std;

using VexType = char;

// 排序使用
template<class Tp>
void Swap(Tp &a, Tp &b)
{
	Tp c = a;
	a = b;
	b = c;
}

// 用于保存每条边的信息
struct Edge
{
	int start;		// 起点的下标
	int end;		// 终点的下标
	int weight;		// 边的权重
	Edge() :start(0), end(0), weight(0) {}
	// 重载运算符< 方便比较
	// 按照权重大小进行比较
	bool operator <(Edge e)
	{
		return (this->weight < e.weight);
	}
};

// 邻接矩阵存储
class Graph
{
public:
	int num_Vex;					// 点数
	int num_Edge;					// 边数
	VexType *VexSet;				// 点集
	int **arc;						// 邻接矩阵
	Edge * e;						// 每条边的信息
public:
	Graph(int numV, int numE);
	~Graph();
	void CreateGraph(int **weight, VexType * v);
	vector<Edge> Kruskal();
};

Graph::Graph(int numV, int numE)
{
	this->num_Edge = numE;
	this->num_Vex = numV;
	
	e = new Edge[num_Edge];

	// 初始化邻接矩阵
	this->arc = new int*[numV];
	for (int i = 0; i < numV; ++i)
	{
		arc[i] = new int[numV];
		for (int j = 0; j < numV; ++j)
			arc[i][j] = 0;
	}
}

Graph::~Graph()
{
	// 省略
}

void Graph::CreateGraph(int ** weight, VexType * v)
{
	// 省略
}

vector<Edge> Graph::Kruskal()
{
	// 对边按权重有小到大排序
	for (int i = 0; i < num_Edge; ++i)
	{
		// 权重最小的边的下标
		int min = i;
		for (int j = i+1; j < num_Edge; ++j)
		{
			// 使用重载的运算符<
			if (e[j] < e[min])
				min = j;
		}
		Swap<Edge>(e[i], e[min]);
	}

	// 用来记录每个顶点是否已经被添加到最小生成树中
	bool *added = new bool[num_Vex];
	// 初始化
	for (int i = 0; i < num_Vex; ++i)
		added[i] = false;

	// 保存最小生成树中的每条边
	vector<Edge> res;

	// 从第1条边开始遍历
	int i = 0;
	while (i<num_Edge)
	{
		// 此边的两个顶点至少有一个没有被添加到最小生成树中
		if (!added[e[i].start] || !added[e[i].end])
		{
			added[e[i].start] = true;
			added[e[i].end] = true;
			// 将此边添加到最小生成树中
			res.push_back(e[i]);
		}
	}
	return res;
}